René Descartes - filosofi och matematik
Descartes liv
 René
Descartes (lat. Renatus Cartesius) föddes 1596 i La Haye
(numera Descartes) i Frankrike. Han studerade vid en jesuitskola i La
Flèche, och möjligen också vid universitetet i
Poitiers. Han gick sedan in i armén av, som han sade,
utbildningsskäl och var stationerad i Nederländerna och
Tyskland.
René
Descartes (lat. Renatus Cartesius) föddes 1596 i La Haye
(numera Descartes) i Frankrike. Han studerade vid en jesuitskola i La
Flèche, och möjligen också vid universitetet i
Poitiers. Han gick sedan in i armén av, som han sade,
utbildningsskäl och var stationerad i Nederländerna och
Tyskland.
En natt hade han en dröm som sade att hans öde var att
grunda en allomfattande naturvetenskap, baserad på matematiken.
Descartes var med om slaget vid Prag, och sedan lämnade han
armén för att resa runt i Europa, bl a hamnade han i
Paris 1628. Här hade Descartes många vänner, men han
kom fram till att han ville bo långt ifrån dem för
att få arbetsro, varpå han flyttade till Holland samma
år.
I Holland levde han under tjugo år i ensamhet, en tid under
vilken samtliga Descartes verk fullbordades och publicerades. De
främsta av dessa är Discours de la méthode
(Avhandling om metoden) 1637 och Meditationes de prima
philosophia (Betraktelser över den första
filosofin) 1641. Genom korta resor till Paris och genom
korrespondens med sin skolkamrat från jesuitskolan i La
Flèche, fader Marin Mersenne (1588-1648), höll Descartes
kontakt med framstående forskare och var därigenom
väl insatt i vetenskapens senaste rön. Mersenne var munk
och sysslade förutom med eget matematiskt arbete också med
att hålla alla vetenskapsmän underrättade om vad alla
andra höll på med.
1633 hade Descartes tänkt ge ut Le Monde (Om
världen), som var ett större verk om de materiella
tingens natur. Här lärde Descartes ut det kopernikanska
systemet, men då han fick veta att Galilei (1546-1642)
förföljdes för att ha gjort detsamma, drog Descartes
in publiceringen av rädsla för jesuiterna. Detta föga
heroiska val var typiskt för Descartes försiktighet mot
överheten. Då han diskuterade med vetenskapsmän var
han däremot obeveklig.
Descartes hade många beundrare, men samtidigt möttes
hans revolutionerande filosofiska och fysikaliska idéer,
naturligt nog, av häftigt motstånd. I Holland blev han
till sist utsatt för en förföljelsekampanj. Descartes,
som ju ville ha lugn och ro, tackade då ja till en inbjudan
från drottning Kristina (1626-89) att komma till Stockholm
för att vara hennes lärare och rådgivare hösten
1649. Under de kalla vintermorgnarna, drottningens lektioner
började klockan fem, drabbades Descartes så
småningom av lunginflammation, och han dog i februari 1650 i
Stockholm.
Descartes filosofi
"Det är inte gott nog att ha ett gott förstånd,
det viktigaste är att använda det väl", sade
Descartes, rationalismens främste portalfigur. Rationalismen
är en kunskapsteoretisk ståndpunkt som hävdar, till
skillnad från den empiriska, att vår kunskap inte
behöver ha sin grund i erfarenheten, utan att den delvis är
medfödd. Vi använder vårt förnuft. Hur vi ska
använda vårt förnuft visar Descartes i
Méthode och Meditationes, där han
förverkligar det han drömt om en natt under sin
militärtid.
Descartes ansåg att en korrekt vetenskaplig metod saknades.
Han ville därför bygga upp en axiomatisk metod. Filosofins
uppgift är att skapa ett säkert fundament, eller som
Descartes kallade det; rötter till kunskapens träd. Fysiken
jämförde han med stammen och t ex mekanik och medicin med
grenar. Men för att bygga upp något måste man
först riva det som finns i vägen, något som Descartes
gör med det metodiska tvivlet.
Man skall bara tro på sådant som vi inte kan betvivla,
hävdade Descartes. Betrakta alltså allt du kan tvivla
på som falskt. Med hjälp av detta ifrågasätter,
eller betvivlar, Descartes sedan olika typer av kunskap. Tron
på auktoriteter betvivlas genom att dessa ibland motsäger
varandra, och därigenom motsäger auktoriteterna som grupp
sig själva. Kunskap byggd på sinnenas vittnesbörd
betvivlas på grund av sinnenas bedräglighet. Hela
yttervärldens existens betvivlas med hjälp av
drömargumentet, som går ut på att vi omöjligen
säkert kan skilja mellan dröm och verklighet. Även
sådana satser som "kvadraten har fyra sidor" och andra
analytiska satser kan betvivlas. Det kan ju vara så att
världen skapades av en ond ande som låter mig tro att
kvadraten har fyra sidor, samtidigt som han skapat världen
så att kvadraten inte har fyra sidor.
Descartes söker igenom allt som går att betvivla, och
finner till sist något som inte går att tvivla på,
nämligen satsen "cogito, ergo sum" (jag tänker,
alltså existerar jag). Det är ju paradoxalt att
förneka både sin egen existens och att man tänker,
eftersom ett förnekande innebär tänkande. Här
anser sig Descartes ha funnit en fast grund, en första princip
för sin filosofi.
Om jag nu är ett tänkande ting med idéer,
så måste dessa motsvara något så att jag kan
dra slutsatsen att det finns en materiell värld oberoende av
mig. Då måste jag bli av med den bedräglige onde
anden, och bevisa att det finns en icke-bedräglig Gud som
ansvarar för de idéer jag har.
Descartes bevisar Guds existens på några olika
sätt. Ett av dessa är följande: Gud uppfattas som
fullkomlig. Det som är fullkomligt saknar ingen positiv
egenskap. Alltså har Gud egenskapen att existera och
alltså existerar Gud. Descartes utnyttjar också ett bevis
som utgår från att allt har en orsak.
Eftersom en icke-bedräglig Gud nu bevisats existera så
kan vi lita på matematiken, genom vilken vi enligt Descartes
kan nå kunskap om den fysiska världen. Vi har nu
gissningsvis nått fram till gränsen mellan rötter och
stam på kunskapens träd.
Descartes matematik
Descartes ansåg att alla vetenskaper borde baseras på
matematiken. Detta var ingen helt ny idé, Pythagoras (569-500
f Kr) och Platon (429-348 f Kr) hade haft liknande tankar.
Decartes ansåg att man skulle endast acceptera
föreställningar som framstod som fullständigt klara.
Den axiomatiska geometriska teori som hade utvecklats av Euklides
(330-275 f Kr) ansåg han var baserad på sådana
klara föreställningar och kunde därför ses som en
modell för all annan vetenskap.
En morgon låg Descartes, sin vana trogen, och mediterade
då han upptäckte en fluga som flög omkring i rummet.
Han kom på att man kunde beskriva flugans läge genom att
ange dess avstånd till tre väggar med ett gemensamt
hörn. Om flugan t ex kröp omkring i taket kunde man
ange dess position genom att ange dess avstånd till två
av sidorna med ett gemensamt hörn på den rektangel som
taket utgjorde. Så var alltså det rätvinkliga eller
cartesiska koordinatsystemet fött. Varje läge hos en punkt
i rummet eller planet kunde beskrivas med tre
(x,y,z) respektive två (x,y)
tal kallade koordinater. En punkt i rörelse kunde beskrivas med
ekvationer.
Descartes förbättrade också den algebraiska
notationen genom att bl a införa exponenter (t ex
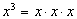 )
och konventionen att beteckna okända kvantiteter med
bokstäver från slutet av alfabetet (t ex
x,y,z) och kända kvantiteter med
bokstäver från början av alfabetet (t ex
a,b,c). Viëte (1540-1603) hade tidigare
börjat använda bokstäver för att beteckna
okända kvantiteter, men han använde en notation som var
ganska ordrik. Ekvationen som med modern (cartesisk) notation skulle
skrivas:
)
och konventionen att beteckna okända kvantiteter med
bokstäver från slutet av alfabetet (t ex
x,y,z) och kända kvantiteter med
bokstäver från början av alfabetet (t ex
a,b,c). Viëte (1540-1603) hade tidigare
börjat använda bokstäver för att beteckna
okända kvantiteter, men han använde en notation som var
ganska ordrik. Ekvationen som med modern (cartesisk) notation skulle
skrivas:
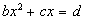
skrev Viëte:
"B in A Quadratum, plùs C plano in A, aequari D
solido." (Notera den klassiska dimensionshanteringen.)
Algebran och aritmetiken lär vid den här tiden varit ett
kaos bestående av en osammanhängande samling recept
(algoritmer) för olika typer av problem. Descartes beskrev olika
metoder för att överföra algebraiska problem till
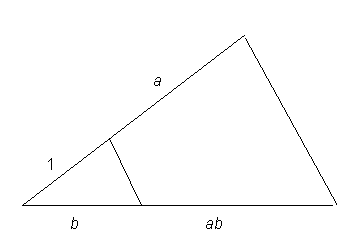
geometriska problem. Han uppfann t ex en metod att geometriskt
multiplicera två längder så att svaret blev en
längd i samma plan. Metoden bygger på likformighet.
Även de andra aritmetiska räknesätten t ex
division och rotutdragningar kunde han utföra geometriskt.
På detta sätt kunde han återföra algebraiska
algoritmer till den säkra geometriska grunden.
Han utnyttjade också att man kunde göra det motsatta
och löste geometriska problem genom att föra in
bokstäver och ställa upp och lösa ekvationer. Denna
metod kallas analytisk geometri.
Han hade kravet att alla problem i princip skulle kunna lösas
med redskap vars delar var länkade så att man visste
förhållandet mellan delarnas rörelser, detta innebar
i praktiken att han endast hanterade polynomfunktioner (t ex
ekvationen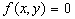 ).
Tidigare hade man dock bara hanterat linjer, cirklar och
kägelsnitt.
).
Tidigare hade man dock bara hanterat linjer, cirklar och
kägelsnitt.
Ett resultat från Descartes är hans teckenregel som
säger att antalet positiva nollställen till ett polynom
(skrivet med termerna i fallande gradordning) maximalt är lika
med antalet skiftningar i tecken hos koefficienterna. Exempelvis
så har
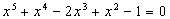
tre skiftningar i tecken och antalet positiva nollställen kan
alltså högst vara tre. Den analytiska geometrin
utvecklades också av den samtida Fermat (1601-65), men han var
tyvärr inte speciellt villig att publicera sina resultat.
Ett tidigt arbete av Descartes var Musicae Compendium
(1618) där han gjorde en del matematiska undersökningar av
musik, t ex varför vissa ackord är mer
välljudande än andra.
I Regulae ad Directionem Ingenii (1628) beskriver Descartes
hur man bör filosofera men det liknar väldigt mycket hur
man löser matematiska problem.
Descartes presenterade sin analytiska geometri i La
Géométrie (1637) som var ett appendix till hans
filosofiska arbete, Méthode. De andra appendixen var
Dioptrique och Météores som handlade om
optik respektive meteorologi. I Dioptrique härledde han
bland annat Snells lag (brytningslagen) med hjälp av en
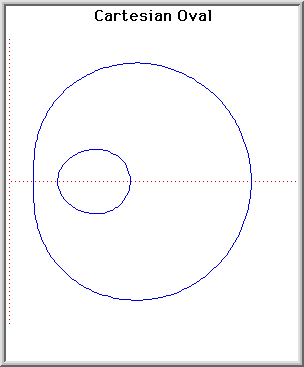
eterteori för ljuset. Han studerade ingående en kurva med
intressanta optiska egenskaper som numera kallas Cartesius oval.
Météores innehåller också en del
om optik eftersom han där förklarade regnbågen,
då utnyttjade han bl a brytningslagen. Det var också
Descartes som förutsåg hur lufttrycket skulle variera med
höjden över havet och han tipsade sin unge vän Pascal
(1623-62) om att undersöka detta. Descartes umgicks också
bl a med Huygens (1629-95) i Nederländerna.
Newtons 1:a lag (tröghetslagen) är ursprungligen
formulerad av Descartes.
Descartes fastställde dagordningen för filosofin och
naturvetenskapen för tvåhundra år framåt.
Källor
- Hamlyn, D. W. (1998). Filosofins historia. Stockholm:
MånPocket.
- Marc-Wogau, K. (1996). Filosofin genom tiderna 1600-talet,
1700-talet. Stockholm: Thales.
- Thompson, J. (1996). W&W:s Matematiklexikon.
Stockholm: Wahlström & Widstrand.
- Benson, H. (1996). University Physics. New York:
Wiley.
- Sällström, P. (1991). Tecken att tänka
med. Stockholm: Carlsson.
- Daintith, J. & Nelson, R. D. (Red.) (1989). The Penguin
Dictionary of Mathematics. London: Penguin.
- Hecht, E. (1987). Optics. Reading, Mass.:
Addison-Wesley.
- Singer, C. (1984). Naturvetenskapens historia. Lund:
Liber.
- Encyclopædia Britannica Online. (1999). Descartes,
René. <http://search.eb.com/bol/topic?eu=115145&sctn=1&pm=1>.
- History of Mathematics. (1997). Descartes.
<http://www-history.mcs.st-andrews.ac.uk/history/Mathematicians/Descartes.html>.
Copyright © 1999-2001 by Mikael
Bonnier &
Henrik
Ihse, Lund, Sweden
 René
Descartes (lat. Renatus Cartesius) föddes 1596 i La Haye
(numera Descartes) i Frankrike. Han studerade vid en jesuitskola i La
Flèche, och möjligen också vid universitetet i
Poitiers. Han gick sedan in i armén av, som han sade,
utbildningsskäl och var stationerad i Nederländerna och
Tyskland.
René
Descartes (lat. Renatus Cartesius) föddes 1596 i La Haye
(numera Descartes) i Frankrike. Han studerade vid en jesuitskola i La
Flèche, och möjligen också vid universitetet i
Poitiers. Han gick sedan in i armén av, som han sade,
utbildningsskäl och var stationerad i Nederländerna och
Tyskland.